Visual Standard 003

Visual Standard 003 was developed to provide a graphical user interface for the Java classes which were necessary to run the simulations for our MISQ article. The underlying model and the results can be found in:

Weitzel, T./Beimborn, D./König, W.: A Unified Economic Model of Standard Diffusion: The Impact of Standardization Cost, Network Effects, and Network Topology. Forthcoming in: MIS Quarterly, Special Issue on Standard Making, 2006. (http://www.misq.org/archivist/forthcoming/accepted.html)

Abstract:

This paper is motivated by the following question: What drives the diffusion of a communication standard and what results can we expect? Past literature provides many instructive but mostly unrelated answers. Frequent findings are startup problems, penguin effects, and tendencies towards monopoly. But substantial problems in applying the models to concrete standardization problems reveal that the dynamics are probably more complex. Not all networks are ultimately conquered by a single standard once it has attracted a certain number of users. And not all diffusion results are either complete or no standardization.

We address the question of the conditions of particular diffusion behaviors by developing a formal standardization model that captures all fragmented phenomena in a unified approach. Drawing from findings of other research we incorporate the structure of the underlying user net-work as an important determinant for diffusion behaviors. The approach allows us to disclose varying conditions that generate frequently observed standardization behaviors as special parameter constellations of the model. Using equilibrium analysis and computer simulations we identify a standardization gap that reveals the magnitude of available standardization gains for individuals and the network as a whole. The analysis shows that network topology and density have a strong impact on standard diffusion and that the renowned tendency towards monopoly is far less common. We also report how the model can be used to solve corporate standardiza-tion problems.

Structure and Manual

GUI Structure

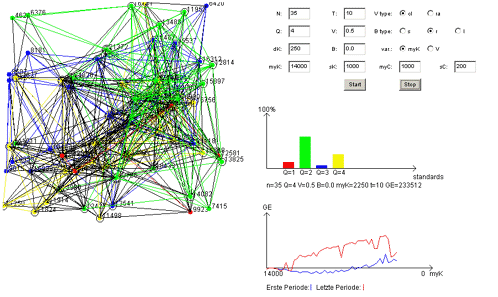
The GUI of the applet consists of four parts: The upper right segment contains the simulation controls: parameterization, start, and stop. The upper left segment visualizes the simulated network. Actors are represented by nodes while neighbourhood relationships are displayed by edges. An standard adopting actor will be colored. If two adjacent nodes have adopted the same standard, the connecting edge will be displayed in the same color. Presented values represent the size of the actor which is defined as the sum of all outgoing communication costs. The actor's size is also displayed by the number of rings.

The middle segment on the right shows the present distribution of standard adoption within the network (in percent). Below the diagram there is a textual output line of all relevant parameters and results. The lower right diagram shows the network-wide net savings (i.e. total communication cost savings cij minus standardization costs Ki) as global measure for network performance. Because it is a multi-period simulation, the results for the first (blue) and last (red) period are given. Please note, that none of both graphs does represent the result of the centralized solution. This would increase computing time tremendously (of course depending on the chosen size of the network). If T (= simulation horizon) is chosen high enough, the red graph represents the total monetary result of the stationary state.

Parameterization

The simulations run with the following parameters:

• Basic parameters
  • n: number of actors
  • Q: number of available standards each actor can choose from
  • T: simulation horizon. For each parameter constellation, a complete scenario over T periods will be simulated. In a T>1 scenario actors can observe decisions of their neighbors and include them into their decision calculus.
  • V: network density. V=1.0 means all nodes being interconnected. V=0.0 means there are no edges i.e. communication costs to be saved between any nodes at all.
  • B: A simulation can start with a pre-installed base. B gives the fraction of actors which are pre-installed. If you simulate a multi-standard scenario (Q>1), only the first standard will be pre-installed.
• Monetary parameters
  • myK (= µ(K) ) and sK (= σ(K) ): parameters of the normally distributed standardization costs. They will be computed for each actor and each standard based on the same normal distribution K_i~ ND(µ(K),σ(K)).
  • myC ( = µ(c) ) and sC (= σ(c) ): parameters of the normally distributed standardization costs. They will be computed for each edge based on the same normal distribution c_ij~ ND(µ(c),σ(c)).
  • dK: increment for reducing µ(K) between the simulation runs (if µ(K) is chosen as variator (see below)).
• Options
  • V-type: topology type. Each actor can either be connected with its geographically nearest neighbors (close topology (cl) ) or with any random actor (random topology (ra)). If a close topology is chosen, at low V communication clusters will evolve .
  • B-type: This selector allows you to choose the actors which will be members of the pre-installed base. You can choose random actors (r), the smallest ones (s), or the largest ones (l). See the paper cited above for implications.
  • variator: as variator you have to choose the parameter which will be varied between the different simulation runs. Varying a parameter represents a simulative sensitivity analysis, i.e. it can be investigated how simulation results vary if varying one particular parameter. For complexity reasons, there is no possibility to vary two or more parameters simultaneously.
    Suitable variation parameters would by µ(K) and V. Both values will be incrementally reduced during the simulations. For reducing µ(K) an increment has to be chosen (dK); V will always be reduced by 0.05.
    Other variation parameters will be added in near future.

The following table shows the allowed domains for the parameters. If the user does not choose a value within the specified ranges, the application will automatically choose the default value (last column of the table) without any warning messages.

Manual

Please take into account the following instructions to control the simulation:

• Before reparameterizing please press the "stop"-button. The simulation starts again when using "start".
• After 50 simulation runs the simulation stops automatically. Before restarting you have to press the "stop"-button anyway. In some environments you have either to press "start" and "stop" several times or maybe you have to re-oben the window. A method to avoid this, ist to stop the simulation unless it finishes the 50 simulation runs.
• If an invalid value is feeded, the respective default value will be used automatically.

The applet was tested within the following environments:

• browsers: MSIE 5 and 6, Netscape 7, Mozilla 1.0.1, Opera 8.02
• Java Runtime: J2SE 1.3, 1.4, 1.5
• OS: Win2000, WinXP, MacOS 10.2

For any problems or comments, please contact Daniel Beimborn. If you get problems with particular parameter combinations, please send a screenshot of the applet.